Codeforces Round #742 Non-Decreasing Dilemma 题解 (Java/C++)

题意：

给你一个数组a。要求你支持以下两种操作：

给你一个x和y，表示把a[x]赋值成y。
给你一个l和r，要求你输出区间[l,r]内，所有不下降子串的数目。也就问你有多少对这样的p和q，使得$l\leq p\leq q\leq r$且$a[p]\leq a[p+1]\leq \dots \leq a[q]$。

题解

这个题目是一个典型的线段树的应用。

如下图所示，我们对于每个区间维护三个属性：1. 满足条件的子串的个数，记为ans；2. 从最左侧开始，最长的连续不下降子串的长度，记为left_size；3. 从最右侧开始，最长不下降字串的长度，记为right_size。

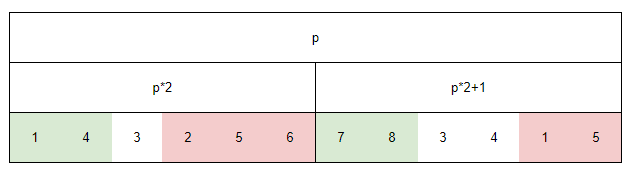
以上图为例，p*2区间的left_size=2；right_size=3。p*2+1区间的left_size=2；right_size=2。

不难发现，p*2区间的右侧和p*2+1左侧可以组合起来。因此$$nodes[p].ans=nodes[p*2].ans+nodes[p*2+1].ans+\\nodes[p*2].right\_size*nodes[p*2+1].left\_size$$也就是说在不考虑p*2区间的右侧和p*2+1左侧可以组合起来的情况时，p的ans就是左右两个儿子的ans之和。
但如果可以组合起来，那就需要加上$nodes[p*2].right\_size*nodes[p*2+1].left\_size$。

代码

Java

C++