Codeforces Round #734 ABCDE 题解

A. Polycarp and Coins

题解

n除以3。如果余数是0，则c1和c2相等；如果余数是1，则c1额外多一个；如果余数是2，则c2额外多一个。

代码

Java

C++

B. Wonderful Coloring - 1&2

题解

模拟即可。

首先每个相同的数，如果超过了k个，则忽略超过k的部分不涂，只涂k种即可。
接着如果某个数恰好有k个，则不用多说，直接涂k种颜色即可。
最后，如果某个数不足k个，则涂完之后接着涂下一个，并且从下一个颜色涂。

以样例为例：

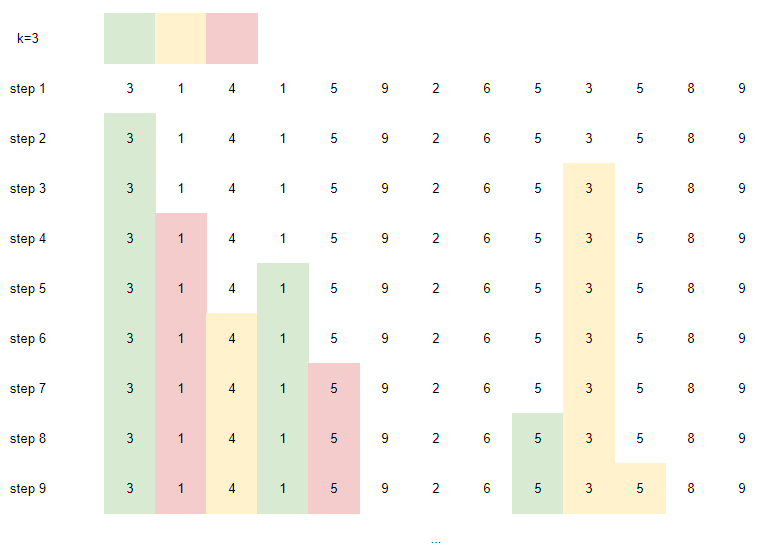
假设我们的涂色的顺序是：绿、黄、红。步骤如下：

把第一个3涂成绿色。
把第二个3涂成黄色。
因为3已经涂完了，于是继续从1开始涂。因为上一个颜色是黄色，所以把第一个1涂成红色。
继续涂1，下一个1循环到了绿色，于是第二个1涂成绿色。
1涂完了，接着涂4。我们把第一个4涂成下一个颜色，也就是黄色。

代码

Java

C++

C. Interesting Story

题解

检查每一个字母，看这个字母最多能支持多少单词。

对于每个字母，我们首先看每个词里面这个字母出现的次数比别的字母多多少（可能为负数）。然后从大到小排序后，依次选词即可。

代码

Java

C++

D. Domino (Easy/Hard)

题解

如果行数为奇数，那么首先将这一行用横向的牌铺满奇数层。如果列数为奇数，那么首先用竖向的牌铺满奇数层。
因为如果行数为奇数，且没有铺奇数层，那么必然存在某一列，剩下的行数为奇数，且需要被竖向的牌铺，而这是不可能的。

在这之后，用同类的牌凑出2*2的方格依次填即可。也是因此剩下的横向牌或者竖向牌的数目必须是偶数。

代码

Java

C++

E. Fixed Points

题解

定义dp[i][j]表示前i个数里留j个数最大符合条件的m。

dp[i][j] = dp[i - 1][j];
if (a[i] == j) {
    dp[i][j] = Math.max(dp[i - 1][j - 1] + 1, dp[i][j]);
} else {
    dp[i][j] = Math.max(dp[i - 1][j - 1], dp[i][j]);
}

也就是说：

如果不选a[i]，则dp[i][j] = dp[i - 1][j];
如果选择a[i]，且这个a[i]恰好是最后一个数，则dp[i][j] = dp[i - 1][j-1]+1;
如果选择a[i]，但是a[i]不是最后一个数，则dp[i][j] = dp[i - 1][j-1]。

最后dp[i][j]在这三个可能中取最大即可。

代码

Java

C++

其他

最近太忙了，F题鸽了。

Codeforces Round #734 ABCDE 题解 (Java/C++)

xloypaypa

A. Polycarp and Coins

题解

代码

B. Wonderful Coloring - 1&2

题解

代码

C. Interesting Story

题解

代码

D. Domino (Easy/Hard)

题解

代码

E. Fixed Points

题解

代码

其他