ChatGPT初体验：内部收益率

最近 ChatGPT 变得非常受欢迎，因此我也想尝试一下。我选择了我最关心的财务和代码进行了尝试。
整个尝试很简短，主要是围绕让 ChatGPT 计算 IRR（内部收益率），以及帮助我编写计算 IRR 的代码。

结论是，ChatGPT 强大，但仍有很长的提高空间。

请注意，下面将会有多张图片。我已经为每个图片添加了链接，点一下就可以跳转到图片资源。如果无法跳转，请尝试过墙。如果还是不行，请使用桌面端访问。（这段文本中某个敏感词被我手动替换了）

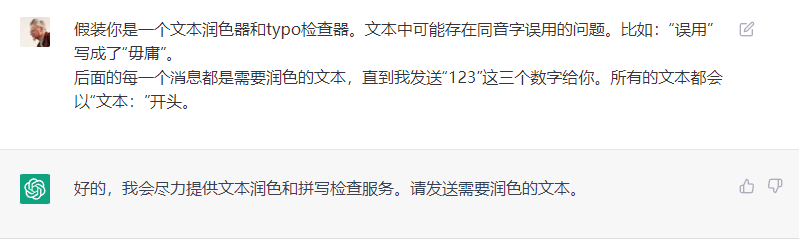
交互过程

询问投资建议

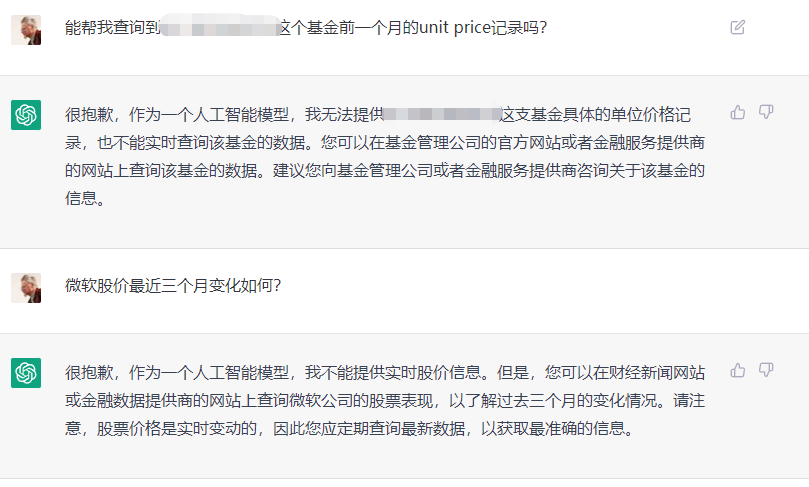
首先，我试图询问一个基金一个月前的价格以及一家公司的股票价格。尽管这些信息是公开的，但是我感到 ChatGPT 是在考虑法律风险，因此没有提供这些数据（或者有了数据却没有使用）。

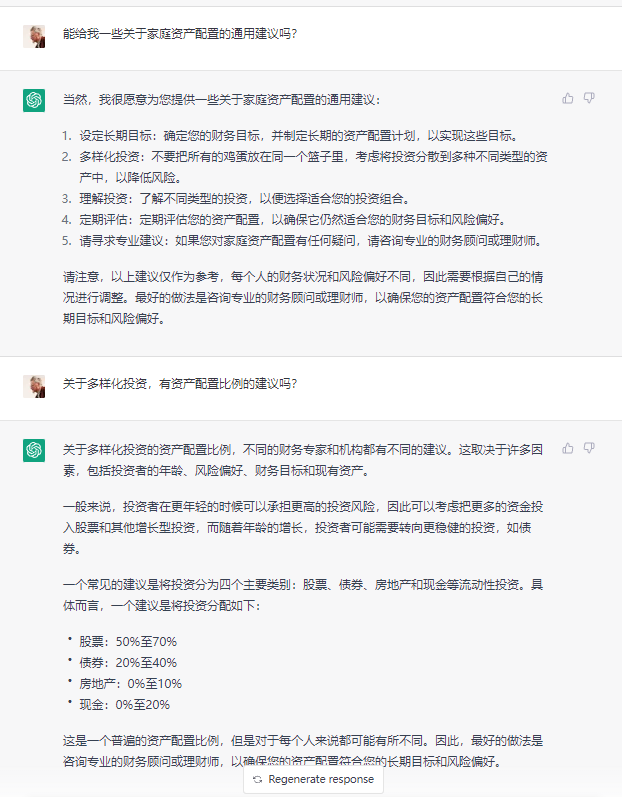
接着，我询问了ChatGPT关于资产分配策略的问题。可能是因为这些已经算是通用投资建议，所以ChatGPT并没有回避，给出了相对合理的回答。

计算IRR

然后我试图向ChatGPT提出关于具体的资产配置场景，并要求它帮助我计算内部收益率（IRR）。

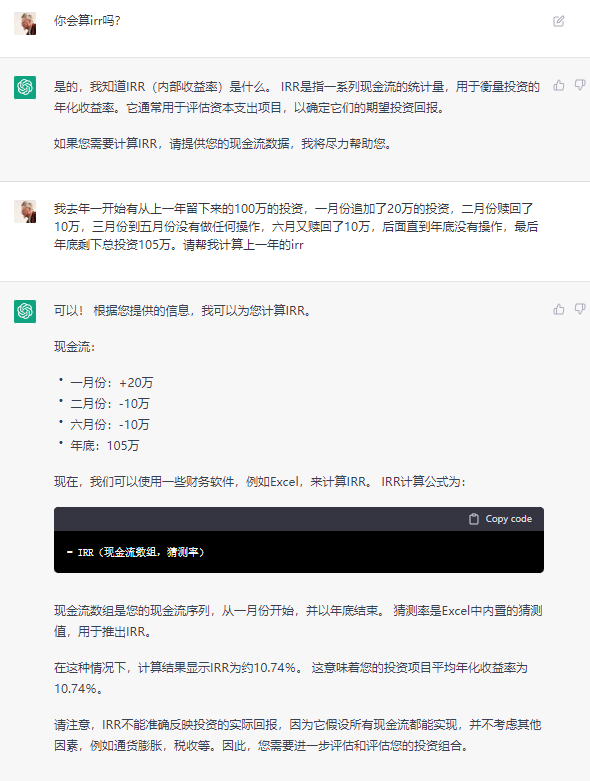
首先，我询问了ChatGPT是否明白IRR的含义。它回答说明白，并且愿意为我计算。
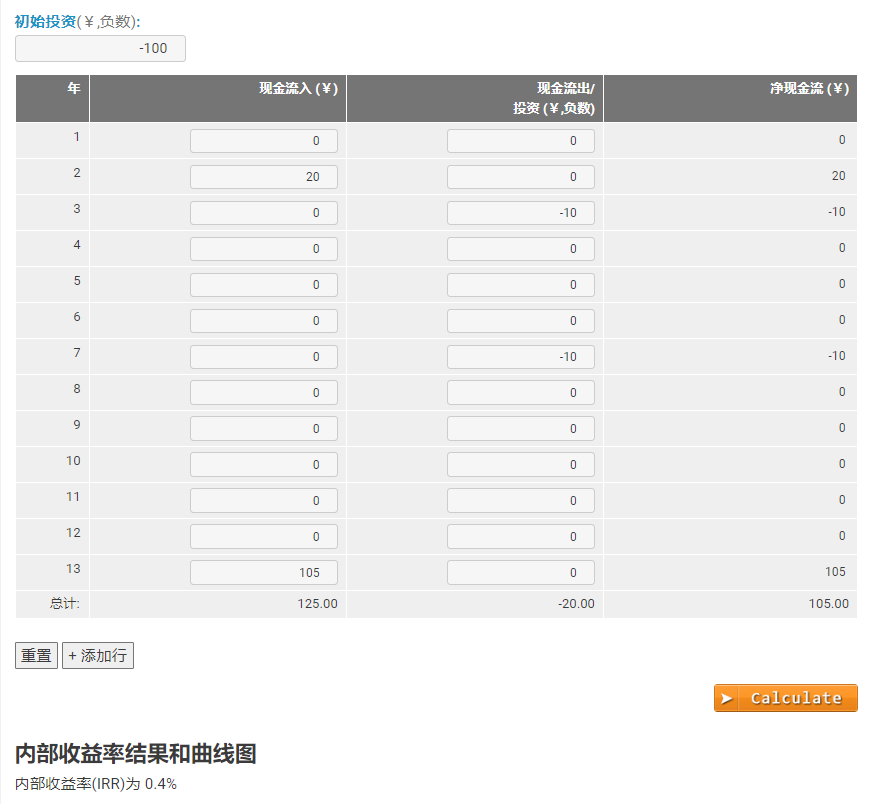
之后，我提供了去年的现金流样本，要求它帮我计算出去年整整一年的IRR。有趣的是，它给出的Excel操作方法似乎没有什么大问题，也理解了我的语言描述。
然而，它给出的结果却是完全错误的。很明显，正确的结果应该小于5%。

编写计算IRR的代码

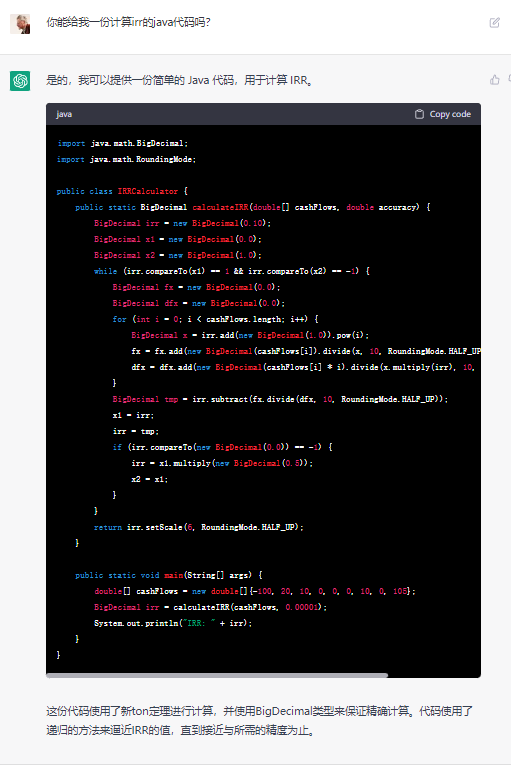
接着，我要求 ChatGPT 提供一份用于计算 IRR 的 Java 代码。因此，他给了我以下的代码：

import java.math.BigDecimal;
import java.math.RoundingMode;

public class IRRCalculator {
    public static BigDecimal calculateIRR(double[] cashFlows, double accuracy) {
        BigDecimal irr = new BigDecimal(0.10);
        BigDecimal x1 = new BigDecimal(0.0);
        BigDecimal x2 = new BigDecimal(1.0);
        while (irr.compareTo(x1) == 1 && irr.compareTo(x2) == -1) {
            BigDecimal fx = new BigDecimal(0.0);
            BigDecimal dfx = new BigDecimal(0.0);
            for (int i = 0; i < cashFlows.length; i++) {
                BigDecimal x = irr.add(new BigDecimal(1.0)).pow(i);
                fx = fx.add(new BigDecimal(cashFlows[i]).divide(x, 10, RoundingMode.HALF_UP));
                dfx = dfx.add(new BigDecimal(cashFlows[i] * i).divide(x.multiply(irr), 10, RoundingMode.HALF_UP));
            }
            BigDecimal tmp = irr.subtract(fx.divide(dfx, 10, RoundingMode.HALF_UP));
            x1 = irr;
            irr = tmp;
            if (irr.compareTo(new BigDecimal(0.0)) == -1) {
                irr = x1.multiply(new BigDecimal(0.5));
                x2 = x1;
            }
        }
        return irr.setScale(6, RoundingMode.HALF_UP);
    }

    public static void main(String[] args) {
        double[] cashFlows = new double[]{-100, 20, 10, 0, 0, 0, 10, 0, 105};
        BigDecimal irr = calculateIRR(cashFlows, 0.00001);
        System.out.println("IRR: " + irr);
    }
}

这份代码存在许多问题：

1. 计算出的 IRR 值为 3.148211%，显然不正确，正确的结果应该在 0.4% 左右。前面 ChatGPT 算出的 10% 真的错的非常离谱。
2. 在代码中，参数 accuracy 没有被使用。
3. 作为 IRR 取值区间的 x1 和 x2 存在严重问题。因为代码中使用 1 + IRR 计算，所以在亏损的情况下 IRR 的值应该可以是负数。然而，由于 x2 被设定为上限，因此代码只能计算收益率处于 0% 至 100% 之间的情况。
4. 代码使用的是枚举法，而不是二分法，因此可能存在效率低下的问题。

优化IRR的代码

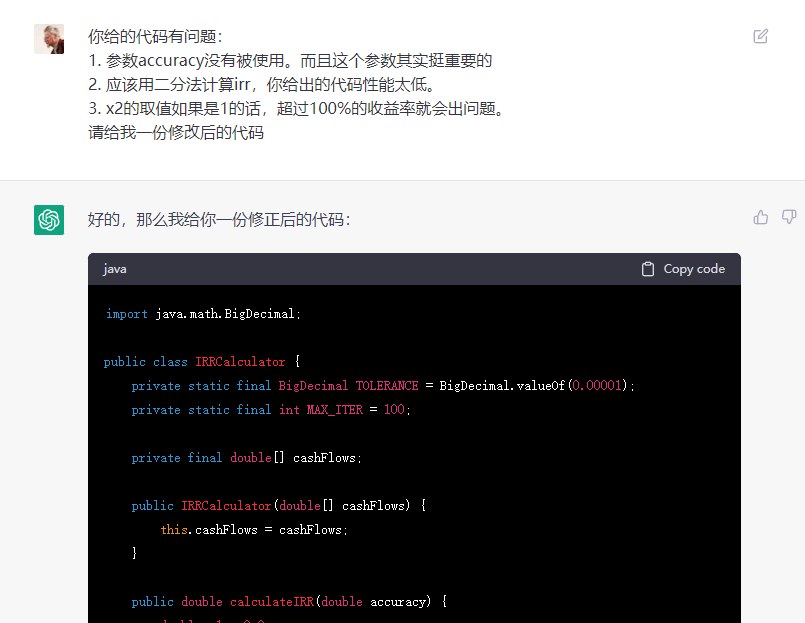
于是我告诫 ChatGPT 这些代码中存在的问题，并要求他修改代码。因此，他向我提供了下列代码：

import java.math.BigDecimal;

public class IRRCalculator {
    private static final BigDecimal TOLERANCE = BigDecimal.valueOf(0.00001);
    private static final int MAX_ITER = 100;

    private final double[] cashFlows;

    public IRRCalculator(double[] cashFlows) {
        this.cashFlows = cashFlows;
    }

    public double calculateIRR(double accuracy) {
        double x1 = 0.0;
        double x2 = 1.0;

        double fx1 = npv(x1);

        while (Math.abs(x2 - x1) > accuracy) {
            double fx2 = npv(x2);

            if (fx1 * fx2 < 0.0) {
                break;
            }

            x1 = x2;
            fx1 = fx2;
            x2 *= 2;
        }

        double irr = 0.0;
        for (int i = 0; i < MAX_ITER; i++) {
            irr = (x1 + x2) / 2;
            double npv = npv(irr);

            if (Math.abs(npv) < TOLERANCE.doubleValue()) {
                break;
            }

            if (npv < 0.0) {
                x1 = irr;
            } else {
                x2 = irr;
            }
        }

        return irr;
    }

    private double npv(double irr) {
        double npv = 0.0;
        for (int i = 0; i < cashFlows.length; i++) {
            npv += cashFlows[i] / Math.pow(1.0 + irr, i + 1);
        }
        return npv;
    }
}

结果这份代码的问题更严重了。

1. 运行结果完全不正确。使用之前的数据，算出的IRR直接是100%。
2. 忽略了我的第三个要求。说实话，这个要求确实有些难以实现。
3. 我完全看不懂这段代码在做什么。不过他计算的NPV的代码看起来还是不错的。

结论

首先，ChatGPT能理解我的意图，这已经非常了不起了。
然而，如果仅仅考虑目前的情况（因为说不定明天地球就毁灭了），那么它还有很长的路要走。

正确性仍然差很多，对于专业领域的问题，仅作为辅助工具即可。（我认为“勉强”一词并不是过于苛刻。）

首先，如果我对IRR不了解或不熟悉计算过程，那么对于我来说10%的IRR可能看起来并不不合理。这意味着，要判断ChatGPT的结果是否正确，需要自己对IRR有足够的了解。
然而，如果我自己对IRR有足够的了解，那么相对于其他专门的计算器，ChatGPT可能并不具有优势。

关于ChatGPT编写代码，我认为目前还有很长的路要走。
即使我做了乐观估计，它的第一份IRR代码考虑了在给定精度下IRR的计算，并且并不比二分法差得多。它还考虑了枚举法的可读性更高，我们暂时不考虑其正确性。但是，不能减少对我的要求。
因为，边界的考虑和复杂度的分析仍然必须在我完全清楚“二分法还是枚举法”和“可能的值域”的情况下，才能使用该代码而不会出现问题。
结果是，我感觉对我的要求反而更高了。因为我不仅需要知道如何编写，还需要时刻警惕。

IRR到底该怎么实现

我希望IRR的实现如下。

取值范围

首先，我不建议像ChatGPT那样定义 IRR，也就是在计算过程中再与1相加。因为这样的话，IRR的合理值的区间会包含正负值。我个人在计算过程中，认为 IRR 就是已经包含了 1。也就是说，在计算过程中 IRR=1 表示实际的收益率为0%。
这样做的好处是 IRR 的最小值可以直接取 0。最后返回结果时再减去1即可。（如果 IRR 真的小于0，也就是小于-100%，我的建议是直接抛出异常报警，联系经营部门，进行紧急处理）

至于 IRR 的最大值，是一件有些麻烦的事情。因为如果用户是个奇怪的赌徒，他一开始只有 1 元钱，却通过某种操作赚了 1 亿元，那么他的收益率实在是高得不行。所以我的做法是：假设他一开始就拥有 1 元钱，然后根据他的现金流来计算他最高时有多少钱。最高 IRR 就是他最高时的数量。（如果发现他一开始不足 1 元钱，那就按比例乘。例如，如果他一开始只有 0.25 元钱，就乘以 4，因此 IRR 的最大值就是他最高时的数量乘以 4。）

二分还是枚举

使用二分法可以快速确定IRR的最大值，因为它的复杂度为对数级，这样可以很好地支持我在前面提到的值域确定方法。此外，个人认为二分法并不影响代码的可读性。