Educational Codeforces Round 111 Excellent Arrays 题解 (Java/C++)

题解

首先，我们注意一下l和r的值域，$l\leq 1$，$r\geq n$。所以，对于前一半的a，可以让$a[i]=i+1$，对于后一半的a，可以让$a[i]=i-1$。因此显然有$F(a)=\left\lfloor \frac{m}{2} \right\rfloor \cdot \left\lceil \frac{m}{2} \right\rceil$。

接着，我们立刻可以发现，其实也可以让$a[i]=i\pm x$。具体x的值有多少种可能呢？有$\min{(r-half, half+1-l)}$种值可以选择。

我们又注意到，当n为奇数时，其实有如下图所示的另外一种可能。同理其的可能数为：$\min{(r-half-1, half+2-l)}$。

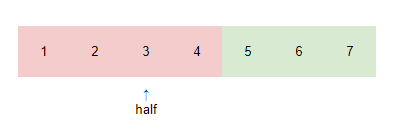
再进一步讨论之前，我们先给出一些定义，我们定义最右端的+x的位置为plus_pos，最左端的-x为minus_pos。于是我们可以得出，对于任意一种排列，x的可能数为：$\min{(r-plus\_pos, minus\_pos-l)}$。

接下来，我们开始讨论minus_pos在plus_pos左边的情况，形如：

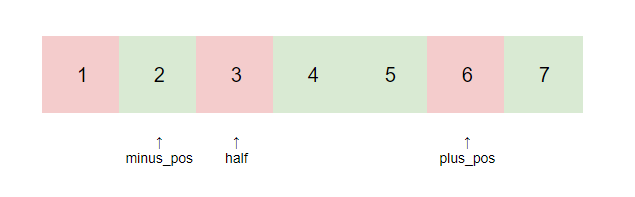
我们可以很自然的想到，我们枚举minus_pos和plus_pos的位置。只要保证$plus\_pos \geq half$以及$minus\_pos \leq half+1$即可。
对于某一对选定的minus_pos和plus_pos，处于两者之间的东西其实可以任意排列。因此，其排列数为：$$C_{plus\_pos\ -\ minus\_pos\ +\ 1}^{still\_need\_to\_plus}$$同时因为$${still\_need\_to\_plus}+{still\_need\_to\_minus}={plus\_pos\ -\ minus\_pos\ +\ 1}$$所以也等于$$C_{plus\_pos\ -\ minus\_pos\ +\ 1}^{still\_need\_to\_minus}$$其中still_need_to_plus表示在minus_pos和plus_pos之间需要是+x的个数。因为plus_pos右边必然全为-x，而minus_pos左边必然全为+x，所以$${still\_need\_to\_plus=n-(minus\_pos-1)-1}$$同理，我们可以类似的给出still_need_to_minus的定义和值。
最后，我们再考虑上x的可能数。于是对于某一对选定的minus_pos和plus_pos，其可能数为：$$C_{plus\_pos\ -\ minus\_pos\ +\ 1}^{still\_need\_to\_plus} \cdot\min{(r-plus\_pos, minus\_pos-l)}$$

但是很遗憾，枚举minus_pos和plus_pos的位置的时间复杂度是$O(n^2)$的。我们仍然需要进一步优化。

我们可以注意到，对于某一个指定的plus_pos，当$minus\_pos\geq r-plus\_pos+l$时，每种排列的x的取值范围始终为$r-plus\_pos$。
同理，反过来指定minuns_pos时，当$minus\_pos\leq r-min\_pos+l$时，x的所有可能数为$minus\_pos-l$。
于是我们想到根据x的可能数来分情况讨论。

对于x可能数取$r-plus\_pos$的情况。此时，只要minus_pos符合条件，-x可以任意选择位置。因此其可能数为：$$C_{plus\_pos\ -\ (r\ -\ plus\_pos\ +\ l)}^{still\_need\_to\_minus} \cdot (r-plus\_pos)$$
以下图为例，假设我们选定了plus_pos=6，同时假设$minus\_pos\geq 2$时，对于任意排列，x的可能数为始终为r-plus_pos。此时由于minus_pos只需要大于等于2即可，同时still_need_to_minus为2（假设我们认为总共要3个-x）。因此总共可以有$C_4^2\cdot (r-plus\_pos)$种可能。

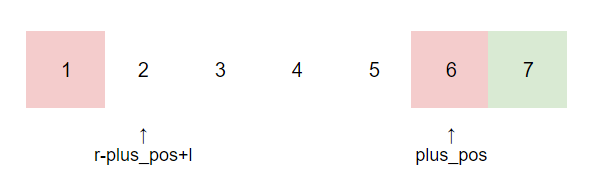
minus_pos-l的情况完全同理。

最后，我们再考虑n的奇偶性。
当n为偶数时，+x和-x的数目始终为$\frac n 2$，因此直接按照上面的做法做就可以了。
当n为奇数时，+x的数目可以为$\left\lfloor \frac{m}{2}\right\rfloor$，也可以为$\left\lceil \frac{m}{2} \right\rceil$。因此两种情况分别按上面做法计算后求和即可。

代码

Java

C++