A. Arena
题意
给你一个长度为n的数组a,表示n个英雄分别的初始登记。现在这些英雄之间随便互相打,等级高的获胜,获胜可以升一级。问多少英雄可以升到$100^{500}$级。
题解
只要这个英雄不是最低等级,就能一直打比他低等级的那个人,然后升级。
代码
C++:

Java:

B. Cat Cycle
题意
有两只猫,第一只从n往1循环跳,第二只从1往n循环跳。如果两只猫试图跳到同一个位置,第二只猫会再往后跳一步。问第k步,第二只猫的位置。
题解
首先把位置从1-n改为0-(n-1),同时第k步改成跳k-1次,这样可以方便取余。
计算第二只猫额外需要走的步数即可。不难发现,当n为奇数时,每$\frac{n-1}{2}$次第二只猫会多走一格。于是就可以算出第二只猫走的总步数,取余后加一即可。
代码
C++

Java

C. Minimum Ties
题意
n个球队踢巡回赛。打平各自得一分,打赢得3分,打输得0分。问,在打平得局数尽可能少得情况下,怎么使n个球队得分数相同。
题解
首先立刻可以想到一种打法:$i$胜过$i+1$。
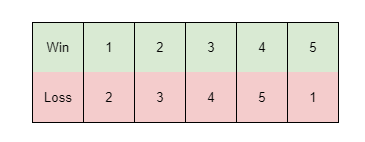
于是我们可以进一步推广这种打法,我每次让$i$胜过$i+diff$,只要能让每个队都赢一轮,就可以保持分数相同。
不难得出,只要剩余得场次多余n场,就一定能打一轮。
代码
C++

Java

D. Pythagorean Triples
题意
问对于$1\leq a \leq b \leq c \leq n$。问满足下列等式的所有可能得abc有多少个:$$\begin{cases}
a^2+b^2=c^2\\
c=a^2-b\\
\end{cases}
$$
题解
可以看到$a^2=c+b$,于是$2\leq a^2 \leq 2\cdot 10^9$。于是我们可以枚举a的值。
将$c=a^2-b$代入$a^2+b^2=c^2$可得,$b=\frac{a^2-1}{2}$。进而可以求出$c$ 的值。
于是我们可以预处理出1到$10^9$之间所有可能的c。然后对于输入的n,我们二分出最大可能的c以及其下标即可。
代码
C++

Java

E. Cheap Dinner
题意
有$n_1$种前菜、$n_2$种主菜、$n_3$种饮料、$n_4$种甜品。每个东西都有一个花费。现在告诉你$m_1$种前菜和主菜不能搭配,$m_2$种主菜和饮料不能搭配,$m_3$种饮料和甜品不能搭配。问你凑出一桌菜最小花费。
题解
首先,先来一个暴力的DP。$dp[i][j]$表示第$i$道菜选择第$j$种菜的最小花费。于是有$dp[i][j]=\min\limits_{1\leq x \leq n_i}{(dp[i-1][x])}+cost[i][j]$。
但直接循环求解$\min\limits_{1\leq x \leq n_i}{(dp[i-1][x])}$一定会TLE。所以需要一种方法快速找出这个最小值。
我们把禁止的搭配按照$y$排序后再按$x$对应的花费进行排序,同时对dp[i-1]按照同样的方式排序。于是我们可以只要找到第一个没有被禁止的$dp[i-1][x]$即可。
代码
C++

Java

