A. Gift Carpet
题解
一列一列顺序匹配即可。
代码
Java

C++

B. Sequence Game
题解
如果$b_i \geq b_{i-1}$那么就不需要做出任何改动直接让$a_i=b_i, a_{i-1}=b_{i-1}$即可。
对于$b_i < b_{i-1}$,那么就只需要在中间插入一个$b_i$即可,也就是:$a_i=b_i,a_{i-0.5}=b_i, a_{i-1}=b_{i-1}$。
代码
Java

C++

C. Flower City Fence
题解
计算水平放置成一摸一样需要的长度即可。比如[4,2,1]如果要用水平放置的话,那么就应该是[3,2,1,1],记为数组b。
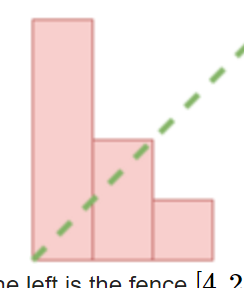
不难发现,对于任意x,如果有c个i使得$a_i \geq x$。那么相应$b_x=c$。
比如,[4,2,1]中,有3个大于等于1,所以$b_1=3$。可得b=[3,2,1]。(对比真正水平放置其实遗漏了最后一个1,但不重要。因为要能一样$a_1$必须等于n)
最后对比一下原数组a和b是不是一样,一样就是YES。否则就是NO。
代码
Java

C++

D. Ice Cream Balls
题解
显然,如果每种冰激凌球只有一个的话,那么x种可以做出$C_x^2$种冰激凌。
因为题目允许两种相同的冰激凌球组成一个冰激凌,所以每种冰激凌球最多可以有两个。并且每有一种冰激凌球有两个,就多一种冰激凌。
所以,x种冰激凌球(每种不限个数)最少可以做出$C_x^2$种冰激凌,最多可以做出$C_x^2+x$种冰激凌。
所以,可以以此分别二分,找到达成目标最少需要多少种和最多需要多少种。然后在这个范围内,暴力枚举每一个x。
对于每一个x,共需要$n-C_x^2+x$个。选最小的即可。
代码
Java

C++

E. Kolya and Movie Theatre
题解
首先,只要不是彻底不看电影。那么只要看了,不考虑$a_i$,单独考虑d的话,那么最后扣心情的总数只由最后一部电影是哪一天看的决定。
比如最后一部电影是第三天看的,那么只需要$-3\cdot d$。之后就和d没关系了。
那么剩下的部分就只是若干个$a_i$的和了。自然我们希望选择一个大于0的,尽可能大的$a_i$。
所以,我们枚举看最后一部电影的日子x。然后用一个优先队列排序x天前的所有$a_i$,如果优先队列长度超过了m,就丢弃队列里最小的。
这样会有个小问题,那就是$a_x$可能并不会被选中。可能实际上最后一部电影是第y天看的。但这样因为多减去了$(x-y)\cdot d$,所以一定不如之前的结果优。
代码
Java

C++

F. Magic Will Save the World
题解
时间限制是4s,而且Codeforces已经不再是一秒只能跑$10^6$的CF了。所以我这个$O(n\cdot \sum{s})=O(n^2\cdot s)$,大概$10^8$的解法也能过,而且只跑了800ms(而且还是Java)。
首先一个01背包,计算出这n个怪物所有可能的总和。
拿到这个总和,二分需要的时间ans。假设需要ans秒,那么就可以再二分找出小于$ans \cdot w$的最大的组合。如果剩下来的怪物需要的f小于$ans \cdot f$,那么ans秒就可以消灭所有怪物。
代码
Java

C++

G. The Great Equalizer
题解
首先,Java用户请谨慎使用Java特性,不然用以TLE。比如下面这个:

首先,不难发现,无论如何,排序后相邻两个数之间的差距每次只会缩减1。
且无论怎么变,较小的数永远不会超过较大的数。最多只会变成一样,然后合并。
所以大小相近两个数要变成一样,且这两个数的差是x,就一定需要x步。
假设b是排序后的a(只是为了说明方便,不需要实际算出来)。
于是问题就转换成了,在每次操作之后,我们要知道最大的$b_i-b_{i-1}$是多少,以及知道最大的$a_i$是多少。
首先最大的$a_i$是很容易维护的,只需要一个set,在每次变的时候把原来的$a_i$删掉,把新的$a_i$加进去就可以了。
最大的$b_i-b_{i-1}$也可以用一个set来维护。
每次变化的时候,把$a_i$相邻的两个数(记为pre_left和pre_right)找到,从set中删除$a_i$-pre_left和pre_right-$a_i$,再把pre_right-pre_left添加进set中,就算是把原本的$a_i$彻底移除了。
接着在去维护$a_i$大小的set中,找到新的$a_i$相邻的两个数(记为next_left和next_right),把next_right-next_left删除,把$a_i$-next_left和next_right-$a_i$添加进set,就算把新的$a_i$彻底加入了进来。
这里需要注意的是,由于$a_i$的值可能重复,$b_i-b_{i-1}$更可能重复。所以两个set不论添加或删除都需要同时记录其数值和下标。
代码
Java

C++



