题解
首先,我们可以立刻发现,对于格子(x,y),不论机器人怎么移动,其格子x+y的奇偶性始终不变。于是很自然的,我们讲奇数和偶数分开求解。
接着我们考虑机器人要如何走才能使次数最少。可以想到的是,机器人一定是从左至右依次拿取。
以下图为例,我们看到机器人优先拿取了(3,3)的糖果。但其结果就是,其左侧(3,1)的糖果一定需要再拿一次。这样就会需要3次。
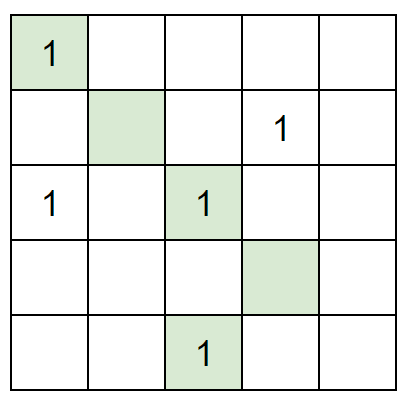
因此上图的策略应该变为(只需要2次):
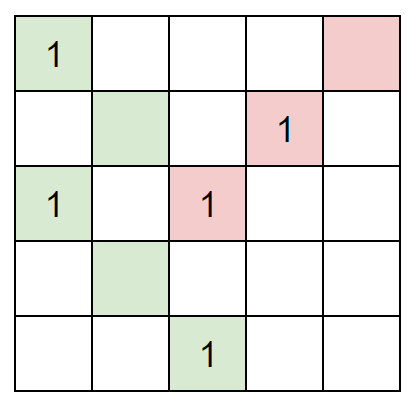
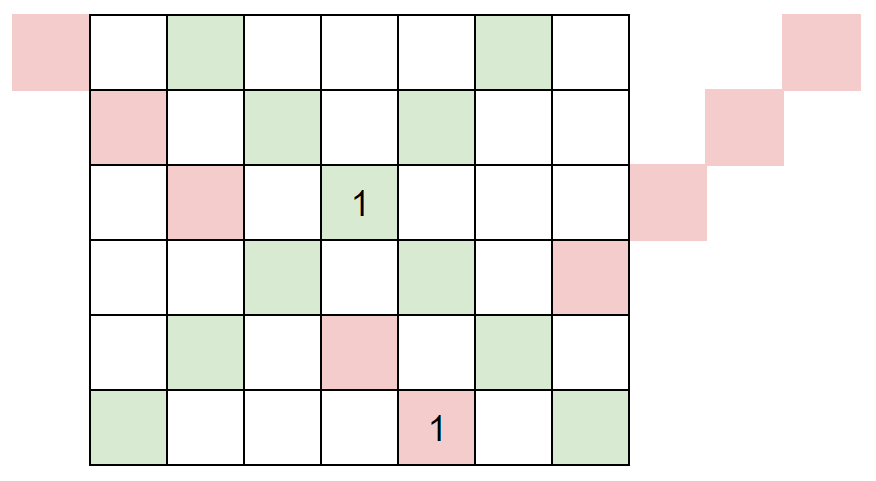
于是我们得到了一定是从左往右拿的结论。现在我们以下图为例,考虑以下问题:相比于(1, 6),是否绿色的1和红色的1都在(1,6)的左侧?
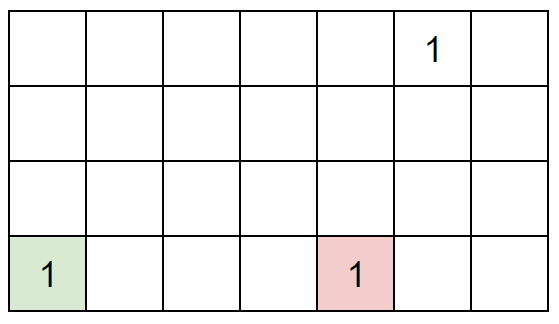
我们从黄色的1出发,就能知道其实绿色的1更“左”一些,而红色的1其实在黄色的1的右边。如下图所示:
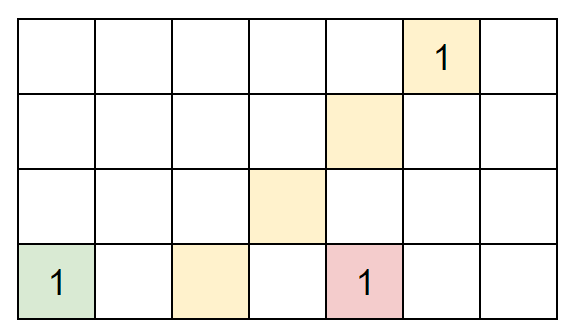
于是,根据从左往右拿的结论,我们定义right_top=y+x。于是我们只需要根据right_top排序即可得到从左往右依次排序的点。也就是说right_top越小,越应该被先拿走。
最后的问题就是,在按照这个策略拿取的情况下,到底需要多少次。我们发现,在上面一张图中,绿色的1是需要一次拿取,而红色的1和黄色的1可以一次拿取。那么我们考虑什么情况下可以一起拿取。
我们定义left_top=y-x。于是我们发现,当且仅当随着x的增加,right_top也随着增加,且left_top随着减小的情况下,可以一起拿。
同时,我们注意到,right_top-left_top越大,说明其x越大。于是,随着right_top增加,如果left_top减小了,那么这个1一定形如上图中红色的1。而如果left_top不仅没有减小甚至增大了,那么一定是落在绿色1的右侧,且一定不能一起拿取。
于是,随着right_top的不断右移(因为我们从小到大排序了),每次我们只需要检查其left_top的右侧是不是有别的1。如果有,那么说明这两个1是一起拿的。
且右侧的1的x一定小于当前1的x。因此我们将原来的1的left_top调整为新的left_top以便后续的1再继续处理。
代码
Java

C++

