Codeforces Round #754 Treelabeling 题解 (Java/C++)

题解

我们首先考虑什么时候$u\oplus v > \min(u,v)$。不难发现，当且仅当在u和v的最高位一个为0一个为1时$u\oplus v > \min(u,v)$。以下图为例：

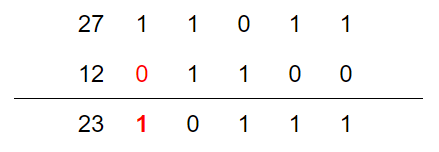
于是我们得到一个很重要的性质：有且只有标号为$2^i$到$2^{i+1}-1$之间的节点可以相互移动。而这个范围共有$2^i$个节点。

于是，我们想到，可以以任意一点为根，维护每个节点的深度。我们可以选取若干组可以互通的数，接着我们再将这些数全部分配到深度为奇数的节点。也就是这些深度节点的总数要恰好等于我们选取的数的数目。
这样因为每次都只能走一步，所以选择任意一个节点都是必胜的。
比如我们选取了两组数：$[2^0, 2^1-1]$和$[2^2, 2^3-1]$。于是我们就需要将1、4、5、6、7这5个数全部分配到奇数层的节点上。如下图所示：

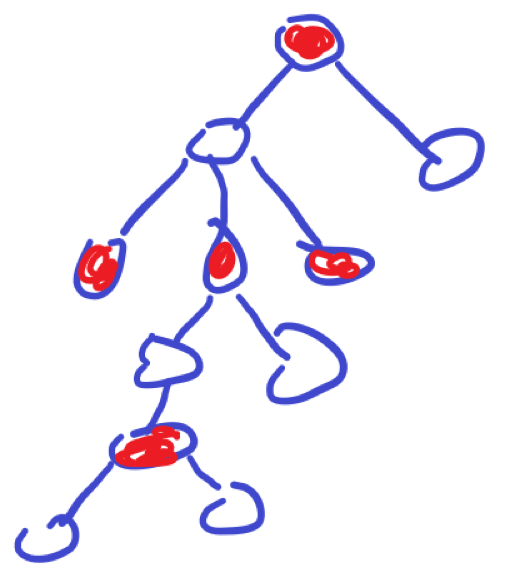
我们只需要将5个数分配到红色的节点即可。

显然，同样的分配针对偶数层也是一样的。因此，如果奇数层的节点数大于一半时，我们就选择偶数层做同样的操作即可。
而一旦需要选出的节点数小于一半，我们就一定能根据所需数目的二进制找出对应的数。比如需要6个数，6的二进制是110。那么我们选择$[2^1, 2^2-1]$和$[2^2, 2^3-1]$即可。

代码

Java

C++