Codeforces Round #751 (Div. 2) Frog Traveler 题解 (Java/C++)

题解

首先，因为到达0之后，就不会再下滑。所以，我们把下滑考虑成跳跃能力的一部分。于是我们重新定义了一次跳跃得行为，把跳跃后下滑，变成了先下滑后跳跃。
于是，很自然的，我们就能得到一次从任意位置i出发，能够跳跃得范围为：$[i-b[i] - a[i-b[i]], i-b[i]]$。
考虑题目中得第三组样例：假设我们从某个位置跳跃到4米。此时，根据题目的定义，应该要下滑1米。于是下一跳是从5米处起跳。但是根据新得定义，我们不用下滑，而是说“从4米处出发，可以跳到0米到5米。”。

这样做得意义在于： 1. 不用考虑下滑。2. 从任意位置出发，都是可以跳到一个连续得区间。3. 这个区间的右值一定大于当前位置（因为$b[i]\geq 0$）。

我们考虑到达0米的前一跳。假设有两个位置都能通过一次跳跃到达0。我们用x和y表示这两个位置，其中x比y距离0更近。
于是我们通过下图可以很明显的发现，y不止能跳到0米，而且能跳到x的位置。（图中黄色部分表示从x出发可以跳跃的范围，红色部分表示从y出发可以跳跃的范围）

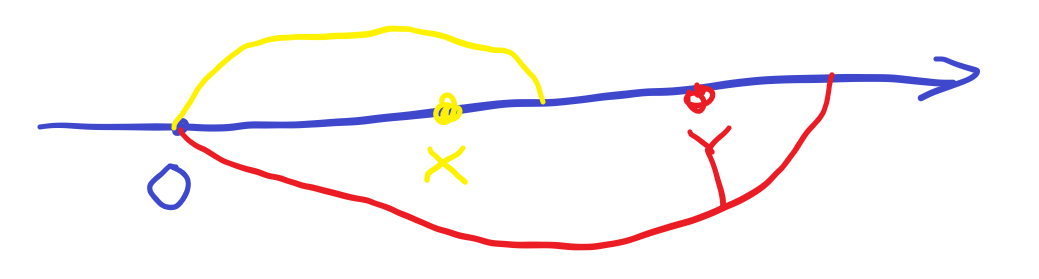
同理，我们考虑能跳跃到x和y的点（也就是我们考虑倒数第二跳），不难发现，能跳到x的，必然也能跳到y。

于是很自然的，我们从now=0出发，每次找到能跳到now的点中最远的那一个。直到跳到n为止。

剩下的问题就是怎么找出所有能跳跃到now的所有的点了。我们可以用类似括号配对的方式，将每个点可以跳跃的范围离散到数轴上即可。

代码

Java

C++