Codeforces Round #750 Pchelyonok and Segments 题解 (Java/C++)

题解

我们以k=3，n=10为例，考虑[l1, r1]的选择，考虑下面两种选择：[4, 6]和[3, 5]。

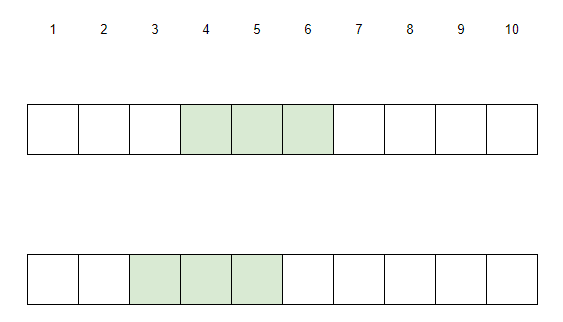
我们先考虑[4, 6]的可行性。根据题目定义，[4, 6]需要找到一个k=2的情况，使得sum(4, 6)<sum(l2,r2)，也就是[7, 8]、[8, 9]、[9, 10]之间至少有一个区间可行，且区间的和大于sum(4, 6)。（其中[9, 10]显然是不可能的）
也就是如下图所示的，要在三个红色的区间中找到一个可行且区间和满足条件。

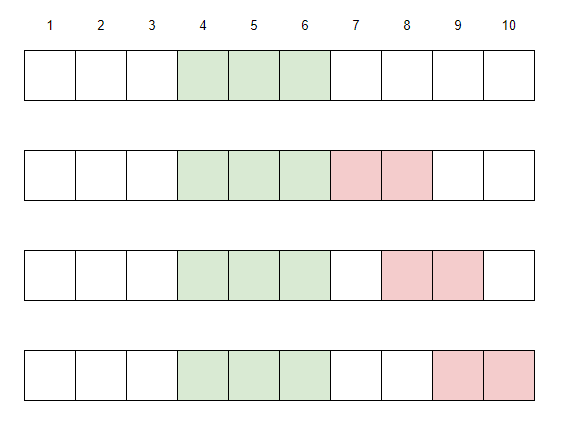
接着，我们对比[3, 5]的可行性。我们得到下图。不难发现，唯一多考虑的区间是深红色的区间。

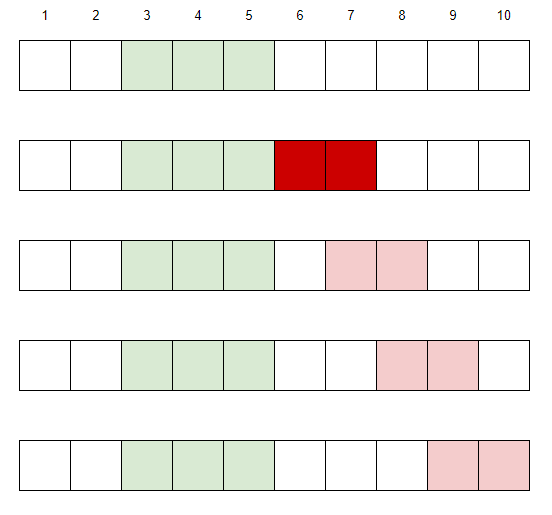
于是不难想到如下dp定义：dp[i][j]表示，k=i时，对于所有可能的l1>=j，最大的可能的sum(l1, r1)的值。于是得到下列状态方程：$$
dp[i][j]=\begin{cases}
dp[i][j+1], & \text{if ($sum(j, j+i-1) > dp[i-1][j+i]$)}\\[2ex]
\max(dp[i][j+1], sum(j, j+i-1)), & \text{if ($sum(j, j+i-1) \leq dp[i-1][j+i]$)}
\end{cases}
$$

最后需要注意两点：

由于dp[i][j]只与dp[i-1][j]有关，因此可以状态压缩。
要注意j的取值范围：$0\leq j$且$\frac {(j+1)*j} 2 \leq n$。

代码

Java

C++