Codeforces Round #746 Hemose in ICPC ? 题解 (Java/C++)

题解

首先，因为gcd(a,b,c)一定小于等于gcd(a,b)或者gcd(b,c)的。因此，这个最大距离必然就是最大的那一条边。

于是不难想到，我们第一次查询所有的点，得到整个树中最大的边的边权。接着二分搜索所有边，如果这一半的边中包含最大的边权，那么就继续在这一半中二分搜索，否则在另一半中二分搜索。

现在的问题就是怎么恰好找出一半的边来查询。

首先我们注意到最后的结果必然是相邻的两个点，且这两个点之间的边权是最大。而我们可以注意到，相邻的两个点必然其中一个是儿子而另外一个是父亲。
于是我们只需要找到这样的一个点，使这个点满足这个条件：这个点到这个点的父节点之间的边权是最大的。

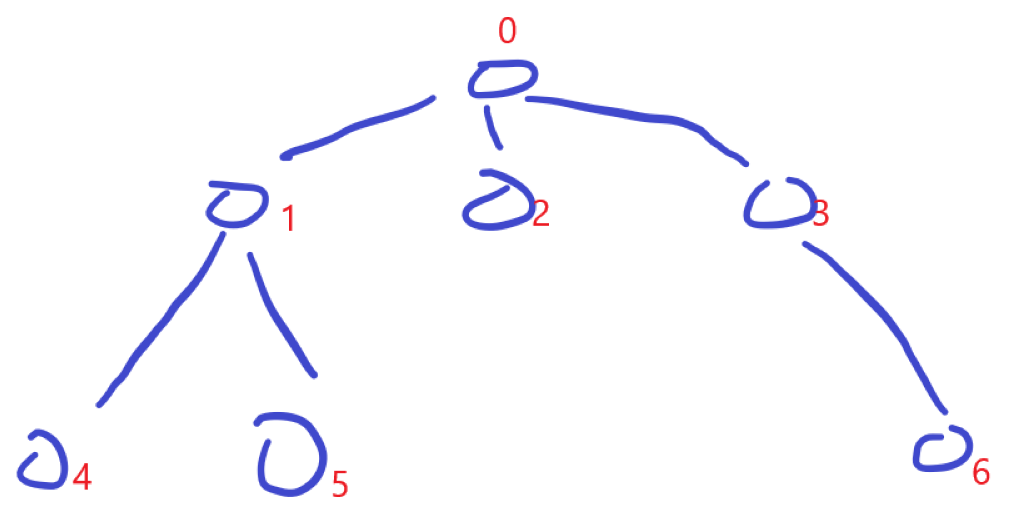
于是就很自然了，我们重新对所有点按照从根向下依次编号（如下图所示）。我们只需要在[1,n-1]的范围内进行二分查找即可（显然，查找时需要包含目标的点的父亲，比如目标是[1,2,3]时，我们需要查询[0,1,2,3]这4个点的id）。

Java

C++