A. Simply Strange Sort
题解
此题按照题目要求模拟即可。
代码
Java

C++

B. Charmed by the Game
题解
首先如果k在结果中,那么n-k也一定在结果中。因为将一开始的主客场交换,那么对于同样的排列,可以得到两个不同的答案。
接着,不妨考虑最小的k的构造方式:显然,我们可以贪心的分配即可。以a=7,b=4为例,我们把奇数场和偶数场分开,我们指定Alice出现在奇数场,Borys出现在偶数场时不会break,于是我们可以如下图分配:
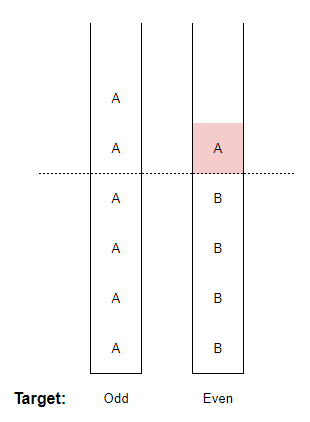
接着,基于上图,我们可以依次交换A和B,如下图所示:
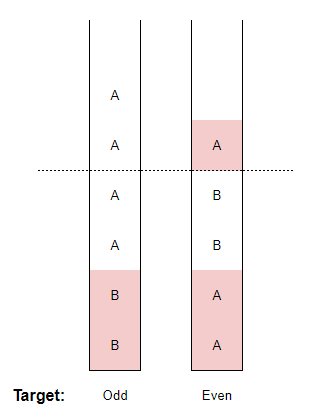
再结合n-k,就能得出所有可能。
代码
Java

C++

C. Deep Down Below
题解
显然,我们可以很容易的得出每个洞穴所需要的最低初始等级。再根据洞穴需要的最低等级进行排序,依次通过,并更新所需要的初始等级即可。
代码
Java

C++

D. Up the Strip
题解
令dp[x]表示,走到x时,有dp[x]种做法。显然dp[1]就是我们要的答案,dp[n]=1。我们依次从n到1计算dp即可。
其实不难发现$dp[x]=\sum_{i=x+1}^ndp[i]+\sum_{j=2}^{x\cdot j <=n}{\sum_{i=j\cdot x}^{j\cdot(x+1)-1}dp[i]}$。
首先考虑较为简单的$\sum_{i=x+1}^ndp[i]$部分。这一部分其实就是第一种操作的可能性。以x=5为例,显然,5后面的所有数都能通过第一种操作到达5。
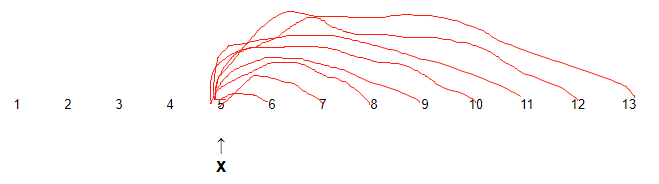
接着考虑$\sum_{j=2}^{x\cdot j <=n}{\sum_{i=j\cdot x}^{j\cdot(x+1)-1}dp[i]}$,也就是第二种操作。我们考虑各个数通过除以j到达x。显然当$j\cdot x \leq y\leq j\cdot(x+1)-1$时,$\lfloor \frac{y}{j} \rfloor=x$。
以x=5,j=2为例,显然10和11,可以通过除以2到达5。再以x=3,j=3为例,9,10,11,12都可以通过除以3达到3。
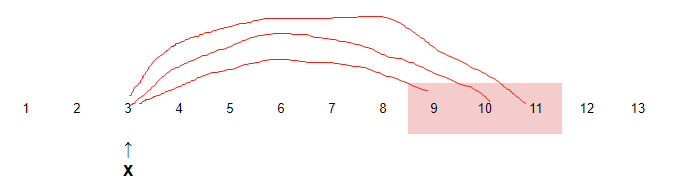
于是很显然,我们维护dp的后缀和,记为f[x]。可以将原dp表达式简化为$dp[x]=f[x+1]+\sum_{j=2}^{x\cdot j <=n}(f[j\cdot x] - f[j\cdot (x+1)])$。
不难发现对于每一个x,j都有$\frac n x$种可能。因此总共需要计算$\frac{n}{1}+\frac{n}{2}+\dots+\frac{n}{n-1}+\frac{n}{n}$,因此其复杂度为$O(n\cdot log(n))$。
代码
Java

C++

E. Bottom-Tier Reversals
题解
显然,因为p只能选奇数。因此,排序前和排序后的下标的奇偶性一定不会发生改变。因此,如果如果发现奇偶性不一致,那么直接输出-1即可。
同时,不难想到,我们一定是从右往左依次排序,且当我们把一个奇数位的值恢复正确时,他前一个偶数位也一定同时恢复正确。因此我们可以依次推论出下列五种场景:
1. 如下图所示,两个数已经倒序在最开头。这种情况,我们直接令p=7进行倒转即可。
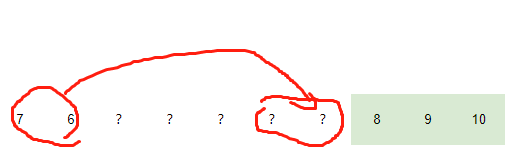
2. 如下图所示,两个数顺序的排在某个不正确的位置。那么我们令p=5,就可以得到第1种情况。
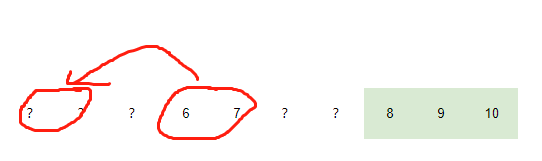
3. 如下图所示,如果两个数逆序排在某个位置。令p=7,我们就可以得到第2种情况。
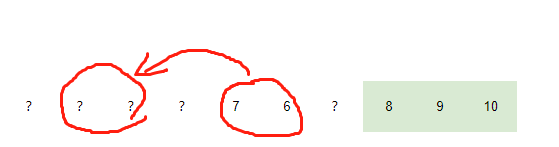
4. 如下图所示,如果两个数不连续,且奇数在第一位。令p=5,我们就能得到第3种情况。
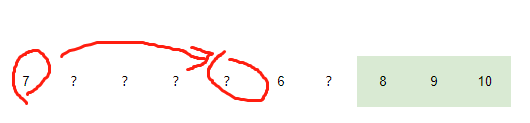
5. 如下图所示,如果两个数不连续,且奇数不在第一位。令p=3,我们就能得到第4种情况。
因此,最多需要5步。而每走完这5步,一定能恢复两位。因此一定能在$\frac 5 2 n$步内完成。
代码
Java

C++

