Codeforces Round #739 ABCDEF 题解 (Java/C++)

A. Dislike of Threes

题解

从1开始依次检查每个数即可。

代码

Java

C++

B. Who's Opposite?

题解

总人数等于$2\cdot |a-b|$，也就是ab之差就是一半的人数。如果abc中任意一个数大于总人数，则输出-1。否则，根据c的情况，加减$|a-b|$即可。

代码

Java

C++

C. Infinity Table

题解

我们按下图方式分段。不难发现，每一段的起始值只差每次都增加2。

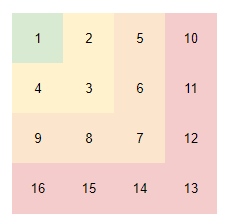
代码

Java

C++

D. Make a Power of Two

题解

枚举$2^0$到$2^63$即可。对于每个$2^k$，我们从高位往低位依次匹配，计算出所需要的操作次数即可。最后我们就从64个答案中选一个最小的。

代码

Java

C++

E. Polycarp and String Transformation

题解

因为每次我们都会从s中删除一个字母。因此我们从后往前遍历t，按照字母首次出现的先后顺序，就可以得到删除字母的顺序。
我们得到了删除的顺序之后，我们就能通过每个字母出现的总数，构建出s。
最后根据我们构建的s，验证一次即可。

我们以样例为例：
如下图所示，我们从右往左检查每个字母首次出现顺序，于是我们得到了删除顺序：lcoayrp。

接着我们尝试构建s。显然，因为l是第一个被删掉的，所以所有的l都应该在s中。接着对于字母c，因为是第二个被删掉的，所以s中的c在t中会出现两次。而对于字母p，s中p的个数为t中p的个数除以7。于是我们就能得到s中每个字母出现的次数。
最后，我们根据s中每个字母的出现次数，再结合t，我们就能得出s。再验证一次即可。