Codeforces Round #729 Strange Function 题解 (Java/C++)

题解

首先我们立刻可以注意到，当i为奇数时，f(i)=2。接着我们开始考量f(i)=3的情况。显然根据定义我们可以知道，只有i为偶数，且i不能被3整除时f(i)=3。
因此我们也可以说：对于所有的i，排除f(i)=2和f(i)=3的情况，剩下的i一定不能被6整除。进一步，当我们考虑到f(i)=4的情况后，剩下的i一定不能被lcm(4,6)=12整除。

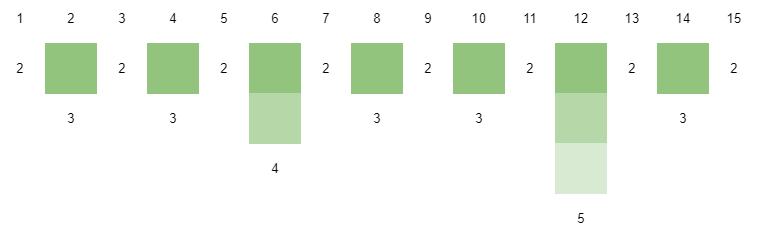
根据上图我们可以发现，2之后剩下的i都满足$i\equiv 0 (mod 2)$。
3之后剩下的i都满足$i\equiv 0 (mod 6)$，也就是6和12。(lcm(2,3)=6)
4之后剩下的i都满足$i\equiv 0 (mod 12)$，也就12和24。(lcm(6,4)=12)

于是，我们只需要依次枚举，每次比较上一次剩下的数目和这次剩下的数目即可。

综上，满足$f(i)=x$的i的个数为$\frac{n}{lcm(1,2,3,...x-1)}-\frac{n}{lcm(1,2,3,...,x)}$。

代码

Java

C++