Codeforces Round #726 Deleting Divisors 题解 (Java/C++)

题解

我们将数字分成三类：奇数、不包括 $2^n$ 在内的偶数，以及 $2^n$ 。于是，经过一步操作我们发现三类数字会有如下转化：

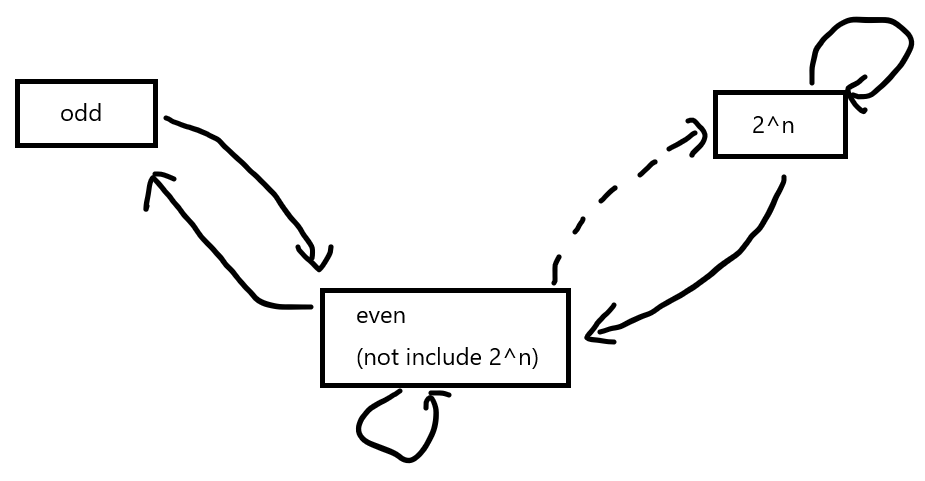
我们看到，对于奇数，一次操作后，必然变成一个偶数。且我们会发现这个偶数一定不是 $2^n$ 。
显然这奇数的所有因数都是奇数，令这个奇数为 $a\cdot b$ 且 $a\cdot b - b=2^x$ 。则我们会发现 $(a-1)\cdot b =2^x$ ，进而必然有 $a-1=2^y$ 且 $b=2^{(x-y)}$ 。于是与b为奇数矛盾。

对于不是 $2^n$ 的偶数，令这个数为 $a\cdot b \cdot c$ ，其中a为偶数，b为奇数，c为任意数。显然有 $a\cdot b \cdot c-b$ 为奇数， $a\cdot b \cdot c-a$ 为偶数。

可以看到，如果任何人拿到一个奇数，那么这个人其实没有选择只能将这个数转化为非2的指数的偶数。而恰巧，我们可以注意到对于素数本身一定会导致失败。于是不论是谁，只要拿到了非2的指数的偶数一定会转为奇数。总有一次这个奇数会是一个素数。
所以，如果Alice拿到了非2的指数的偶数，则Alice必胜，否则Bob必胜。

对于 $2^n$ 。因为非2的指数的偶数是必胜状态，因此一定不会向这个方向转化。于是每次都是减去 $2^{n-1}$ 以得到另一个2的指数。于是取决于指数次幂的奇偶性来判断胜负。

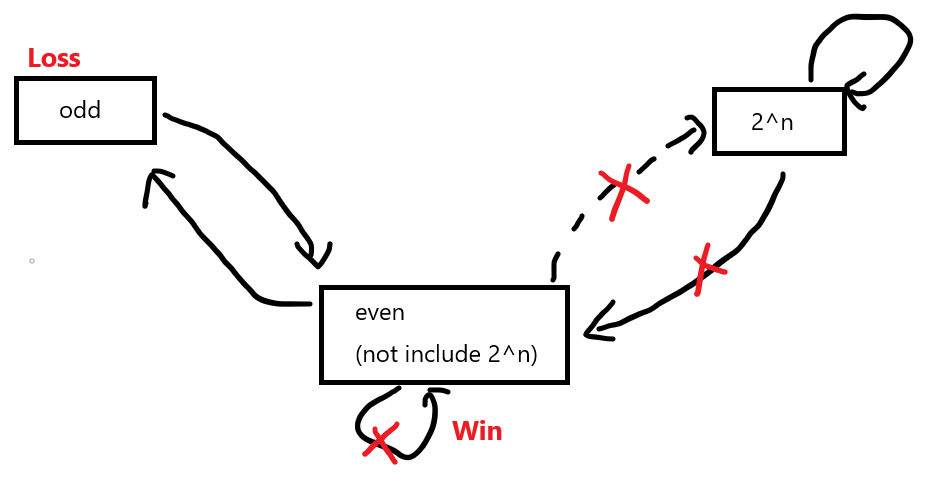
综上，对于Alice我们可以得到下面的图：

代码

Java

C++