题意
给你一颗树。现在对于任意的k,问你有多少对u,v使MEX(u,v)=k。其中MEX是说,这两个点之间的最短路的所有点的下标中第一个没有出现的数。
题解
以0做树根。DFS统计每个节点的子节点(包括自己)总数,记为count。
对于k=0就很显然。也就是只要不经过树根即可。那么显然结果是$\sum_{child}{C_{child.count}^2}$。
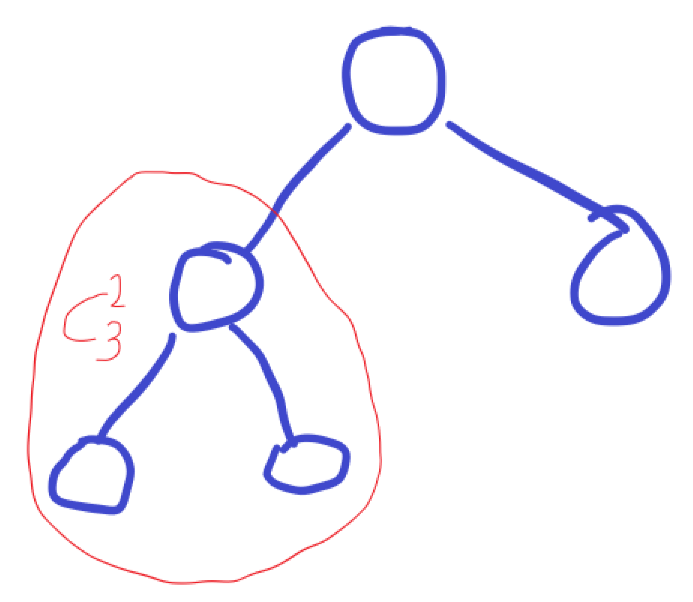
对于k=1。就是一定要经过树根,且不经过1。那么任意一条边,直接和其他的任意点匹配即可。
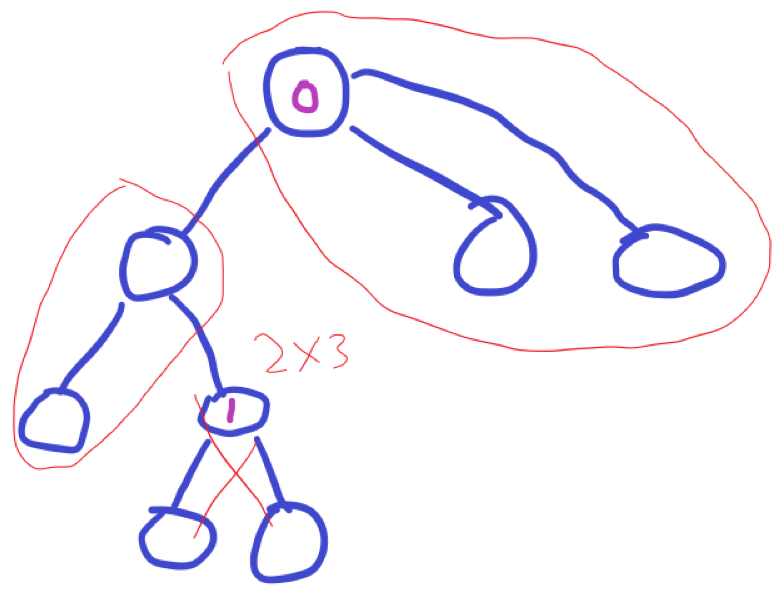
对于其他情况,显然u和v构成的路径必然覆盖0-(k-1)中的所有点。也就是说,如果一旦0-(k-1)存在分支,那么后面就一定都是0。
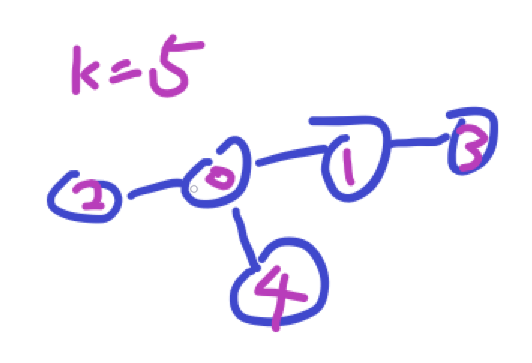
于是在1之后,我们维护这个链的两端。每次都是从两端出发各自选一个点组合起来即可。
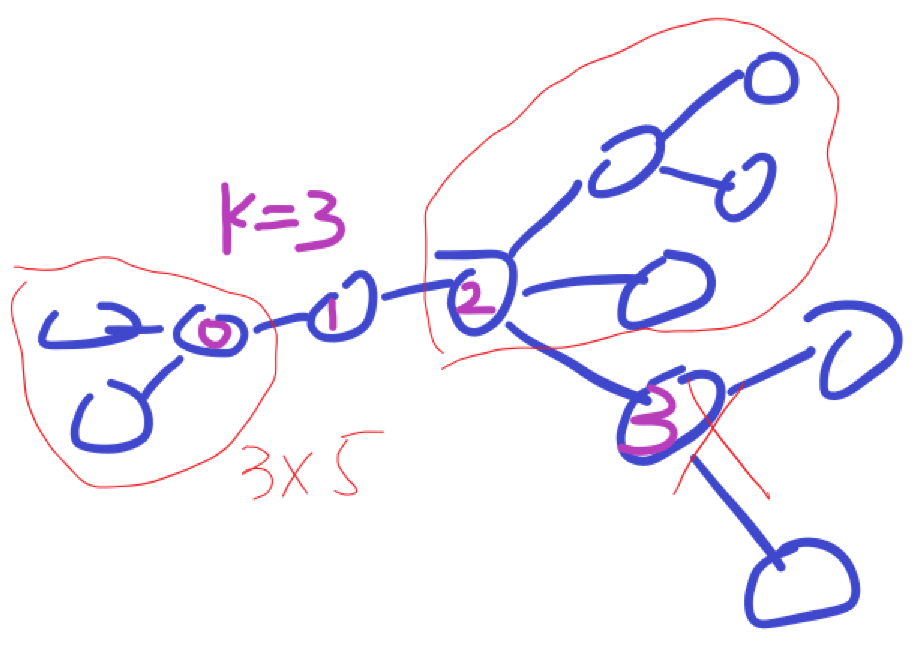
代码
Java
Submission #117023767 - Codeforces
Codeforces. Programming competitions and contests, programming community

C++
Submission #117027176 - Codeforces
Codeforces. Programming competitions and contests, programming community

