题意
给你一个长度为$n$的数组$a$。现在你可以做任意次如下操作:找到任意$i$,$j$和$x$,使$a_i=a_i-x$,$a_j=a_j+x$。也就是把值从$i$给$j$。这个操作的的开销是$x\cdot{|}j-i|$,且之后$i$不能从别的地方获得值,$j$不能给其他地方值。
定义美的数组为:数组中的每个数都是一样的。定义平衡的数组为:通过若干次上面的操作后成为美的数组所花费的最大开销和最小开销相同。
问你$a$的全排列中,有多少个平衡的数组。
题解
由于可以做任意次操作,为了简化问题,我们可以把$x$指定成1。
首先,显而易见的,如果$a_i>avg(a)$,那么$a_i$一定会给出值;如果$a_i<avg(a)$,那么一定会接受值;如果$a_i=avg(a)$,那么一定不会做任何操作。
考量为什么最大值和最小值会相同,我们可以观察下面这张图:
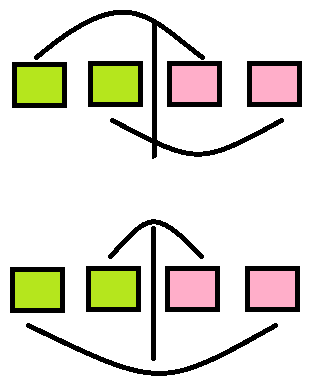
最大值和最小值一样的原因是因为,对于任意一次操作,对于上图来说,交换以下顺序并不会导致开销变化。因此当且仅当所有低于均值和高于均值的部分分别处于两次时,可以平衡。
然后还有一个特殊情况就是,红色或者绿色部分只有一块的时候。这个情况不论怎么排列都可以。
最后,需要注意的是,如果数值多次出现,那么要把这些数的所有排列数除掉。
代码
Submission #112949098 - Codeforces
Codeforces. Programming competitions and contests, programming community

