Codeforces Round #737 Ezzat and Grid 题解 (Java/C++)

题解

这个题大概分为四个部分。

第一部分：Hash

由于最多只有m段1，因此我们很自然的想到将$1\leq l \leq r \leq 10^9$的hash到$1\leq l \leq r \leq 2\cdot 3\cdot 10^5$。将原先的线段的两端离散后排序，按照大小顺序依次hash即可。
代码中对应的函数为：map_point。

同时，这里我们把这m段，分散到对应的行中，以便后续使用方便。
代码中对应的函数为：group

第二部分：DP

我们发现，于其寻找最少删多少行，不如寻找最多能构造出多少行。于是我们能够自然的想到一种$O(n^2)$的DP。

我们令$dp[i]$表示前行，最多能构造出多少行。于是很自然的$dp[i]=\max(dp[j]+1)$，其中$0<j<i$且第i行和第j行能相通。

但是显然，这个是$O(n^2)$的时间复杂度，且每次判断第i行和第j行是否相通的最朴素的做法是$O(m)$的。

第三部分：线段树

首先我们思考，判断第i行和第j行是否相通的标准是什么？如果i行和j行相通，那么至少有一个位置都是1。因此，如果我们把j中的所有区间在i中查询区间最大值，如果某一个区间的查询结果不为0，则i和j必有相通之处。
以下图为例：

j会在i中查询[0,1]以及[5,6]，其中[0,1]的查询结果为1，[5,6]的查询结果为0。因此j和i至少有一处同为1。

进一步，我们结合上面的DP部分，我们发现可以用类似的方法。

对于$dp[i]$，我们的核心问题是，要往前找到某一行j，使得其$dp[i]$尽可能大，且i和j有共同的1。
于是每当我们求出一个新的dp[i]，我们都将i为1的位置更新到线段树中，更新的值为dp[i]。其中这颗线段树要维护的是区间最大值。
至于如何求出新的dp[i]就很明显了。我们只需要查询i行所有为1的区间，取其中最大的值即可。
以样例2为例：

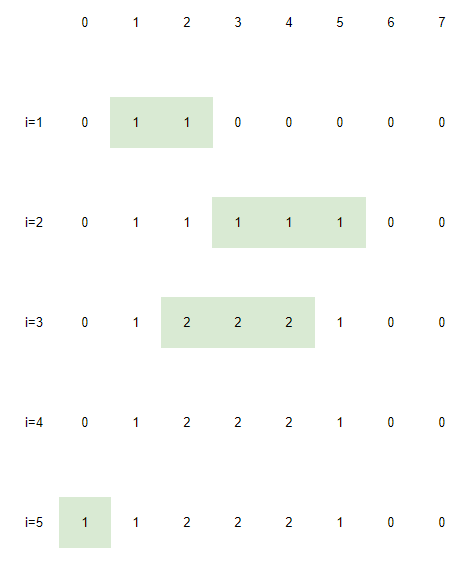
当我们求dp[3]的时候，我们可以在i=2中查询，发现可以查询到的最大值为1。于是dp[3]=1+1，接着将[2-3]更新为dp[3]。

第四部分：记录路径

在线段树维护最大值时，同时维护是哪一行更新了当前区间的最大值。这样，在更新dp[i]时，可以记录下其前置的j到底是谁。这样我们就能依次找出最长的列，剩下的元素都是要被删除的。

代码

Java

C++