Codeforces Round #722 Kavi on Pairing Duty 题解 (Java/C++)

题解

令dp[i]表示n=i时的答案。我们以n=4为例说明解法。

首先考虑两种特殊情况，如下图所示：

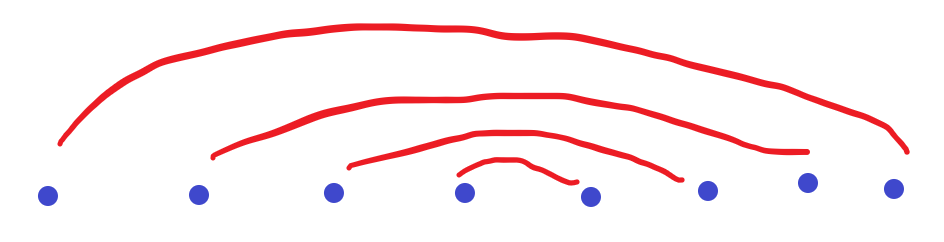
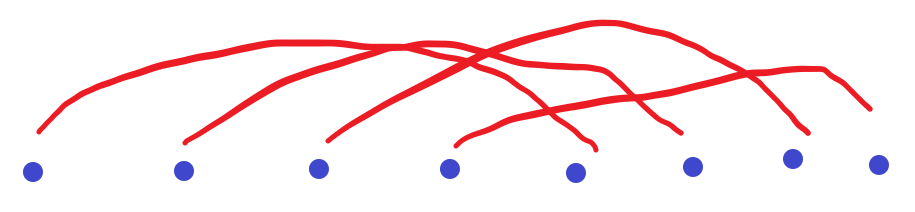
如果外面包一层。则我们可以立刻想到dp[n]=2+dp[n-1]+?

接着，如果包两层。则我们知道dp[n]=2+dp[n-1]+dp[n-2]+?

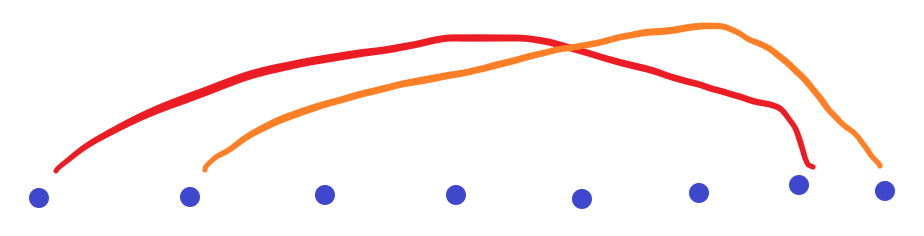
以此类推，可得$dp[n]=2+\sum_{i=1}^{n-1}{dp[i]}+?$

现在还有最后一种可能：将n=4拆成两个n=2且每一段的长度都一样的情况。因此每有一个n的因数就有一个新的解。

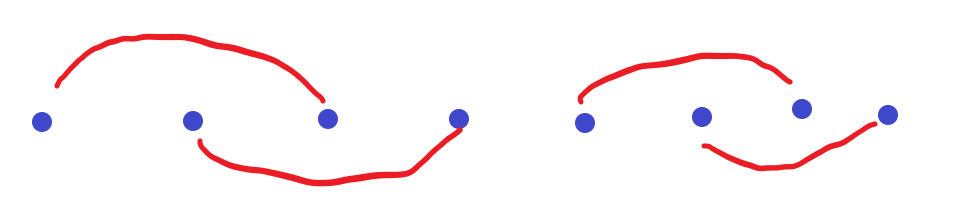
综上，$dp[n]=2+\sum_{i=1}^{n-1}{dp[i]}+count\_of\_factor[n]$。

代码

Java

C++